Removing outliers
Posted on 28th May 2015
So, linear regression isn't so exciting. What about removing outliers? I do find this, just a little, magical:
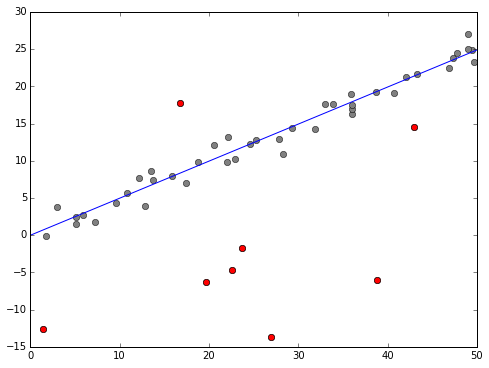
We define a model where a data point \( y_i \) can either be from a normal linear regression model, or just a random (normally distributed) number. We then build into our model indicators \( o_i \in \{0,1\} \) to indicate if this is an outlier or not. Then sample the posterior distribution with an MCMC sampler, integrate out the \(o_i\) and you have your line of best fit. Fix \(i\) and integerate out everything but \(o_i\) and you get an estimate of probability the point is an outlier. The above plot shows those points estimated above 90%.
Rest is in an Ipython notebook on GitHub. This also gave me a chance to play with my own modified Gibbs sampler, which works nicely, if I say so myself.