Graphs in Windsor
Posted on 7th September 2015
While spending a long weekend in Windsor, we found the following:
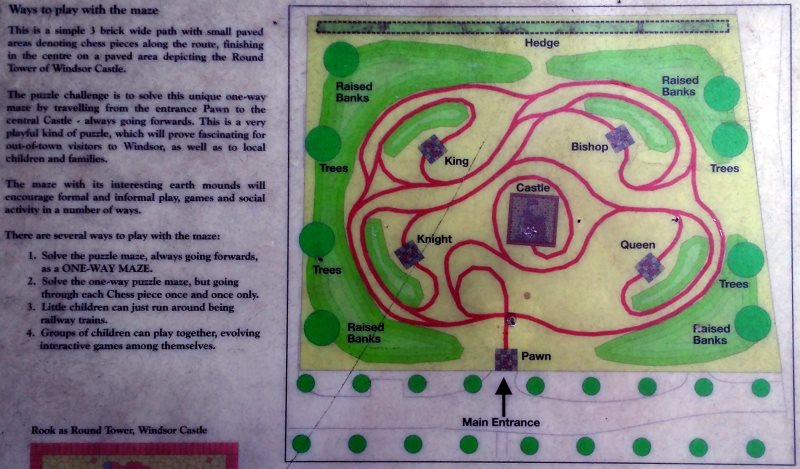
The instructions read, in part:
The puzzle challenge is to solve this unique one-way maze by travelling from the entrance Pawn to the central Castle -- always going forwards.
It's not quite clear to me what this means, but there is a good quote from Here:
The maze should be played as if you are a runaway train - always moving smoothly through the points forwards, and never able to reverse. This maze-movement idea was inspired by the nearby Windsor Railway Station, which brought the Royal Family to Windsor from Victorian times onwards. The maze paths sometimes run together in pairs, like a pair of railway tracks; sometimes they even run through "railway cuttings", where the grass surface rises and falls around them.
I wonder if there is an elegant way to convert this to a directed graph problem? I couldn't see how to do this cleanly, as in the problem you must pass through a "node", not reverse direction.
Anyway, here is a solution. From the pawn you initially get yourself into an outer "loop", from which only the King is accessible. As we can only visit the King once, we don't want to get back onto the outer loop in the same direction.
- So, we take the loop which the King is on, and reverse direction. Two choices here.
- We can then either go to the Bishop:
- In we pass out by the "Raised Banks" then we're back on the outer loop, which is no good.
- So we must reverse direction again, and head in the direction of the Knight.
- We can skip past the knight back onto the outer loop, but that's wrong.
- So visit the Knight.
- Then take the branch down to the Queen, and then to the Castle. Task complete.
- Or we loop back down towards the Pawn, and either:
- Head towards the Knight, but we can't visit the Knight, so we end up back up near the Bishop, and we've just taken a loop.
- Take the earlier branch, and head up the Castle, but following the track, we're forced to visit the Queen, and then head to the Castle. But we've missed pieces.
So, the only solution is King, Bishop, Knight, Queen, Castle. And once we've heading to the Knight, we only have a choice of which direction to pass through the Knight "station" in, everything else is determined. Before that we can loop about a bit if we wish.